Instance Normalization

重新回忆一下标准化的公式：

$$ \hat{x_i}=\frac{x_i-\mathrm{E(X)}}{\sqrt{\mathrm{Var(X)}+\epsilon}} $$

各种不同标准化方法的区别基本上仅在于统计量的计算范围。Instance Normalization会对每一个样本的每一个通道都计算一个统计量，最后得到的统计量个数就是 $N\times C$ ，即样本数乘以通道数。

Instance Normalization和Batch Normalization一样，在pytorch中做了1d、2d和3d的区分，对应的类以及给入数据的size如下表：

类别	大小
`torch.nn.InstanceNorm1d`	$(C,L)$ 、 $(N,C,L)$
`torch.nn.InstanceNorm2d`	$(C,H,W)$ 、 $(N,C,H,W)$
`torch.nn.InstanceNorm1d`	$(C,D,H,W)$ 、 $(N,C,D,H,W)$

InstanceNorm1d

InstanceNorm1d的输入大小有两种取法： $(C,L)$ 、 $(N,C,L)$ ，其中 $N$ 表示样本的个数、 $C$ 表示通道数、 $L$ 表示通道的长度。

在计算均值、方差这两个统计量时，范围是各个样本的各个通道。也就是说，对于输入大小 $(C,L)$ 、 $(N,C,L)$ ，计算出的统计量个数分别为 $C$ 、 $N\times C$

验证如下：

C, L = (3, 4)
data_np = np.random.randn(C, L).astype(np.float32)
data_torch = torch.from_numpy(data_np)

instance_norm1d = torch.nn.InstanceNorm1d(C, affine=False, track_running_stats=False)
instance_norm1d(data_torch)

avg = []
var = []
for channel in range(C):
    avg.append(data_np[channel,:].mean())
    var.append(data_np[channel,:].var())
avg = np.array(avg)
var = np.array(var)
avg = avg.repeat(L).reshape((C, L))
var = var.repeat(L).reshape((C, L))
(data_np - avg) / np.sqrt(var)

InstanceNorm1d验证结果

N, C, L = (2, 3, 4)
data_np = np.random.randn(N, C, L).astype(np.float32)
data_torch = torch.from_numpy(data_np)

instance_norm1d = torch.nn.InstanceNorm1d(C, affine=False, track_running_stats=False)
instance_norm1d(data_torch)

avg = []
var = []
for sample in range(N):
    for channel in range(C):
        avg.append(data_np[sample,channel,:].mean())
        var.append(data_np[sample,channel,:].var())
avg = np.array(avg)
var = np.array(var)
avg = avg.repeat(L).reshape((N, C, L))
var = var.repeat(L).reshape((N, C, L))
(data_np - avg) / np.sqrt(var)

InstanceNorm1d验证结果

InstanceNorm2d

InstanceNorm2d的输入大小有两种取法： $(C,H,W)$ 、 $(N,C,H,W)$ ，其中 $N$ 和 $C$ 的含义不变、 $H$ 表示一个通道的高、 $W$ 表示一个通道的宽。显然此时一个通道的大小就是 $H\times W$ ，即要对每 $H\times W$ 个数值求出一个统计量，算出的统计量个数对于 $(C,H,W)$ 和 $(N,C,H,W)$ 分别为 $C$ 、 $N\times C$

事实上， $(C,H,W)$ 其实是只输入一个样本的情况，和输入N个样本其实没有什么区别。

验证如下：

C, H, W = (2, 3, 4)
data_np = np.random.randn(C, H, W).astype(np.float32)
data_torch = torch.from_numpy(data_np)

instance_norm2d = torch.nn.InstanceNorm2d(C, affine=False, track_running_stats=False)
instance_norm2d(data_torch)

avg = []
var = []
for channel in range(C):
    avg.append(data_np[channel,:,:].mean())
    var.append(data_np[channel,:,:].var())
avg = np.array(avg)
var = np.array(var)
avg = avg.repeat(H * W).reshape((C, H, W))
var = var.repeat(H * W).reshape((C, H, W))
(data_np - avg) / np.sqrt(var)

InstanceNorm2d验证结果

N, C, H, W = (2, 3, 2, 4)
data_np = np.random.randn(N, C, H, W).astype(np.float32)
data_torch = torch.from_numpy(data_np)

instance_norm2d = torch.nn.InstanceNorm2d(C, affine=False, track_running_stats=False)
instance_norm2d(data_torch)

avg = []
var = []
for sample in range(N):
    for channel in range(C):
        avg.append(data_np[sample,channel,:,:].mean())
        var.append(data_np[sample,channel,:,:].var())
avg = np.array(avg)
var = np.array(var)
avg = avg.repeat(H*W).reshape((N, C, H, W))
var = var.repeat(H*W).reshape((N, C, H, W))
(data_np - avg) / np.sqrt(var)

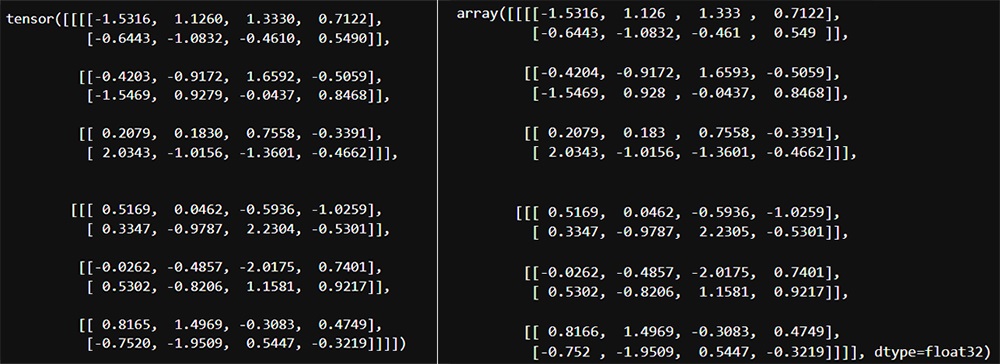
InstanceNorm2d验证结果

InstanceNorm3d

想必到这里Instance Normalization的计算方法已经十分显然了，就是对每一个样本的每一个通道各自独立计算均值和方差，其中的每个数值使用自己所在通道的统计量进行标准化即可。

InstanceNorm3d输入样板的每个通道大小为 $(D,H,W)$ ，对于 $(C,D,H,W)$ 和 $(N,C,D,H,W)$ ，计算得到的统计量分别有 $C$ 组、 $N\times C$ 组

验证如下：

C, D, H, W = (3, 2, 2, 4)
data_np = np.random.randn(C, D, H, W).astype(np.float32)
data_torch = torch.from_numpy(data_np)

instance_norm3d = torch.nn.InstanceNorm3d(C)
instance_norm3d(data_torch)

avg = []
var = []
for channel in range(C):
    avg.append(data_np[channel,:,:,:].mean())
    var.append(data_np[channel,:,:,:].var())
avg = np.array(avg)
var = np.array(var)
avg = avg.repeat(D*H*W).reshape((C, D, H, W))
var = var.repeat(D*H*W).reshape((C, D, H, W))
(data_np-avg)/np.sqrt(var)

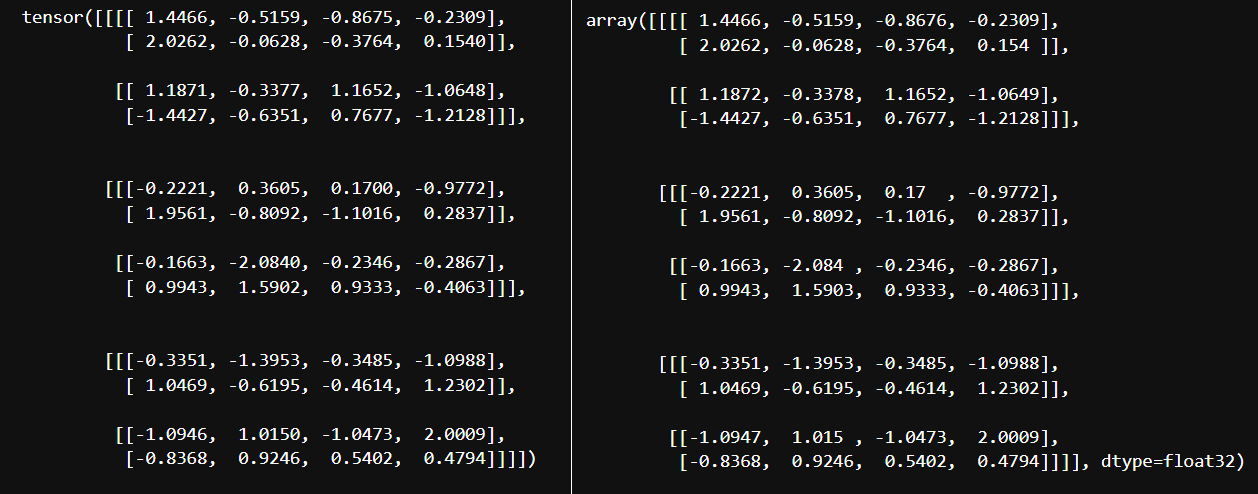
InstanceNorm3d验证结果

N, C, D, H, W = (2, 3, 2, 2, 4)
data_np = np.random.randn(N, C, D, H, W).astype(np.float32)
data_torch = torch.from_numpy(data_np)

instance_norm3d = torch.nn.InstanceNorm3d(C)
instance_norm3d(data_torch)

avg = []
var = []
for sample in range(N):
    for channel in range(C):
        avg.append(data_np[sample,channel,:,:].mean())
        var.append(data_np[sample,channel,:,:].var())
avg = np.array(avg)
var = np.array(var)
avg = avg.repeat(D*H*W).reshape((N, C, D, H, W))
var = var.repeat(D*H*W).reshape((N, C, D, H, W))
(data_np - avg) / np.sqrt(var)

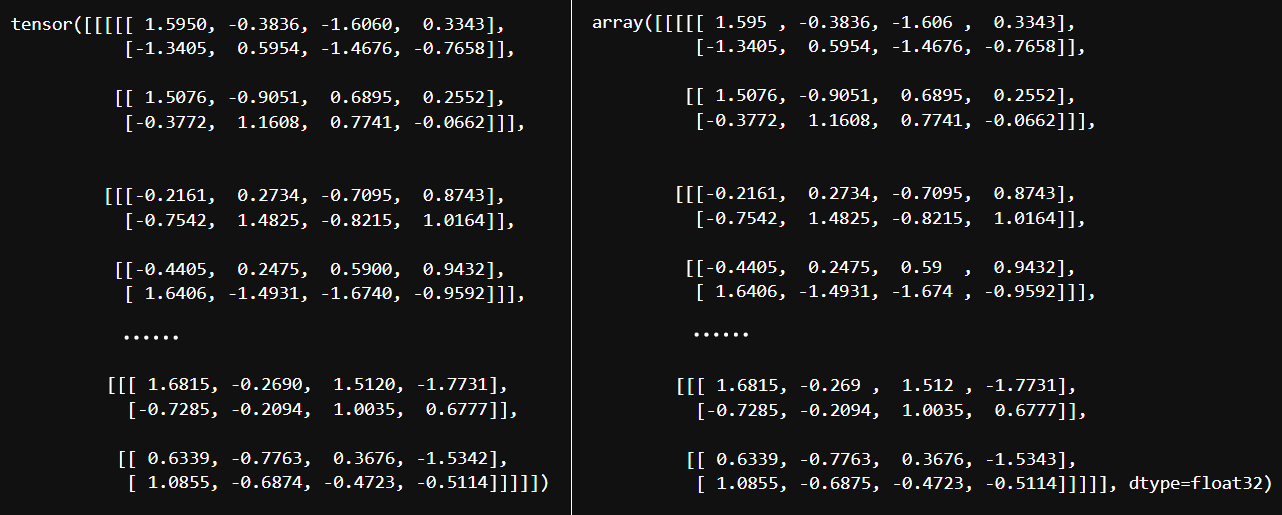
InstanceNorm3d验证结果

总结

根据上面的验证可以发现，1d、2d、3d是根据通道的维度来决定的，通道的维度是多少就使用多少的InstanceNorm

第i个样本的第c个通道的统计量计算如下：

$$ \mu_{i,c} = \frac{1}{J\times K\times \dots}\sum_{j,k,\dots}{A_{i,c,j,k,\dots}}\\ \sigma_{i,c}^2=\frac{1}{J\times K\times \dots}\sum_{j,k,\dots}{(A_{i,c,j,k,\dots}-\mu_{i,c})^2} $$

事实上，就是固定住样本和通道两个维度，对所有其他维度遍历求值：

参与每个统计量计算的数值数量=一个通道中所含数值的数量；
统计量的组数=样本数量✖每个样本的通道数量

类别	大小
`torch.nn.InstanceNorm1d`	\((C,L)\) 、 \((N,C,L)\)
`torch.nn.InstanceNorm2d`	\((C,H,W)\) 、 \((N,C,H,W)\)
`torch.nn.InstanceNorm1d`	\((C,D,H,W)\) 、 \((N,C,D,H,W)\)