Swin Transformer详解
2024-08-02发布于深度学习 | 最后更新于2024-08-06 13:08:00
简介
Swin Transformer是2021年提出来的一个模型,原文为:
Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
该模型主要设计用于视觉领域,有如下特性:
- 使模型的计算量与图片尺寸(\(height\times weight\))线性相关,而不是与图片尺寸的平方相关。
- 参数量便于扩展,适用性强。
- 引入了patch和window机制,使得特征图呈分层形式。正是由于这个设计,计算量与图片尺寸线性相关。
- 引入了shifted-window机制,以提高各层注意力之间的关联性,并进一步提高计算效率降低预测latency
各模块详解
下文以自上而下的方式解构Swin Transformer
Swin Transformer Block
Swin Transformer的基本构成块,细节与各步的输入输出尺寸如下图所示:

细节说明如下:
| 符号 | 含义 |
|---|---|
| \(B\) | Batch,即batch数量 |
| \(L\) | Length,借鉴NLP中的概念,对图片来说值等于\(H\times W\) |
| \(C\) | Channel,即channel数量 |
| \(H\) | Height,图片的高度,即行数 |
| \(W\) | Width,图片的宽度,即列数 |
| \(n\) | 每个batch中的window个数,数值上\(n=\frac{H\cdot W}{wH\cdot wW}\) |
| \(wH\) | window height,即窗口的高度 |
| \(wW\) | window width,即窗口的宽度 |
- 该block的输入尺寸为\(B\times L\times C\),输出尺寸也为\(B\times L\times C\)
- windowlize为窗口化操作,输入、输出尺寸分别为\(B\times H\times W\times C\)、\(B\cdot n\times wH\times wW\times C\)
- windowAttention为以窗口为基本单位的注意力计算机制,输入输出均为\(B\cdot n\times wH\cdot wW\times C\)
- merge window前一步变成了一维的window重新转换为二维的,实现上单纯通过view完成,输入输出分别为\(B\cdot n\times wH\cdot wW\times C\)、\(B\cdot n\times wH\times wW\times C\)
- dewindowlize为逆窗口化操作,即从窗口为基本单位转换到二维图,输入输出尺寸分别为\(B\cdot n\times wH\times wW\times C\)、\(B\times H\times W\times C\)
- 若前后输出输入尺寸不一,则默认将前序步骤输出通过
torch.view适应后序步骤的输入 - 官方实现中MLP非常简单,仅包含了两个Linear层
windowlize & dewindowlize
窗口化操作,论文中提出了shifted-window的操作,如下图所示:
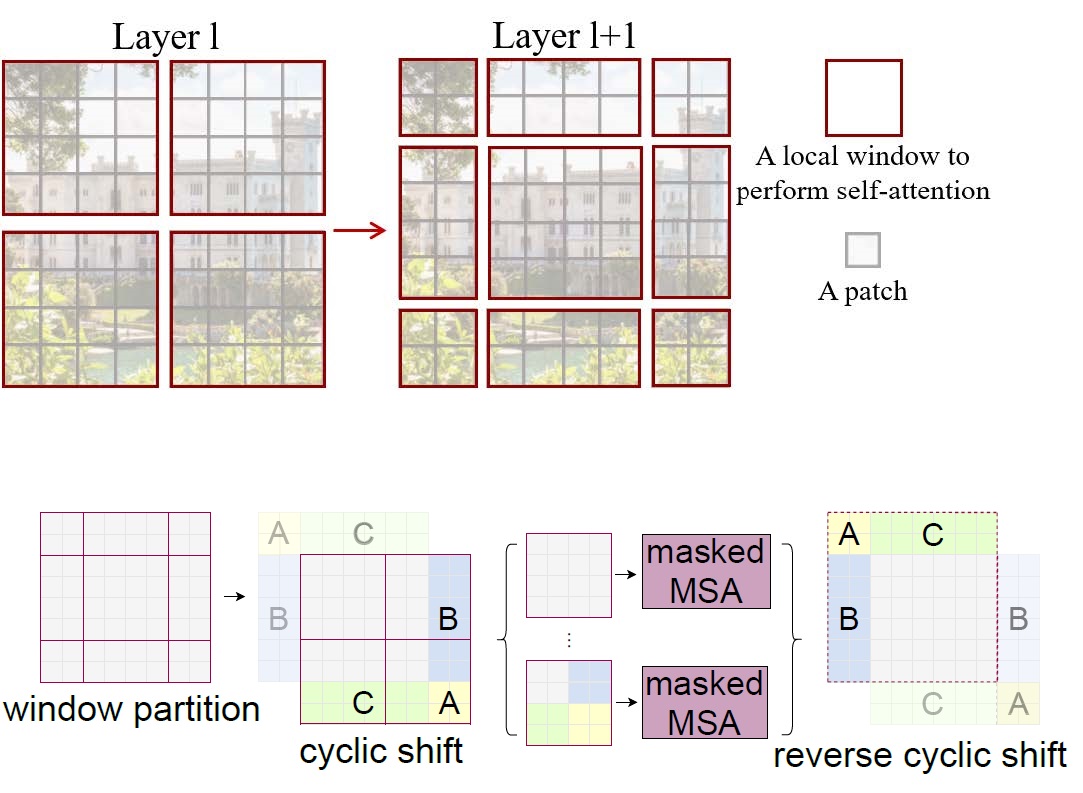
每一个红框表示一个window,作为基本单位参与MSA(multi-head self attention)计算。由于偏移后各window大小不同,就采用了循环偏移cyclic shift方式,本文实现中通过torch.roll完成向左上循环偏移,并保持各window大小相同。但如此会导致事实上不相邻特征之间的自注意力计算,本文在计算attention时使用mask(即在要mask的位置-infinite)解决这一问题。
循环偏移完成后,进行了一系列的维度变换以完成窗口“化”,如下图所示:
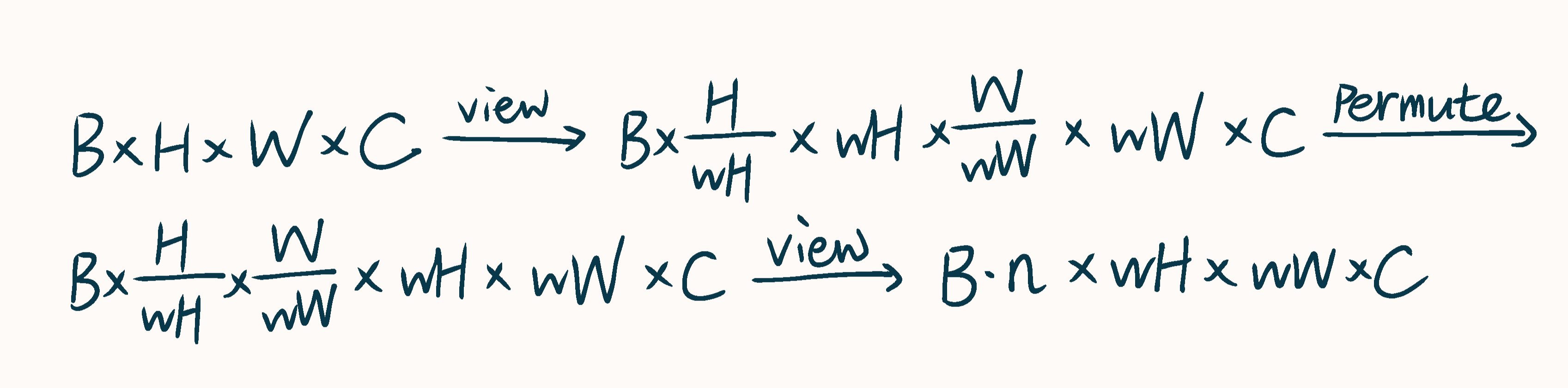
windowlize就是先循环偏移、再维度变换;dewindowlize就是先维度变换、再循环偏移,逆转过程与方向即可。
原文所附代码中还包含了合并循环偏移和维度变换操作的cuda实现
window attention
以window为基本单位的self attention计算,主体过程如下图所示:
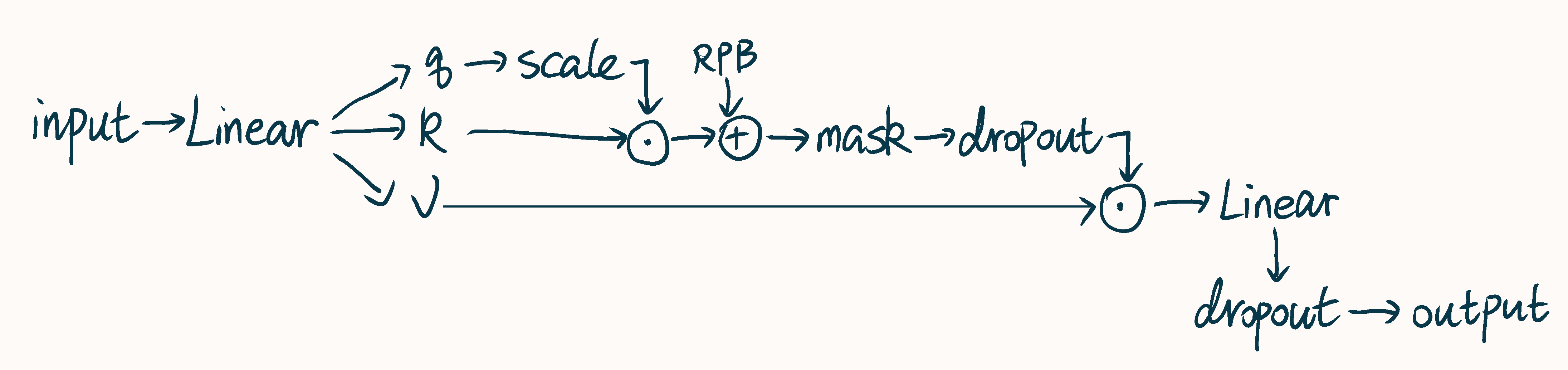
细节说明如下:
| 符号 | 含义 |
|---|---|
| \(h\) | 注意力的头数 |
- 该attention的输入输出尺寸均为\(B\cdot n\times wH\cdot wW\times C\)
- 整体结构与普通的attention没有什么太大的区别,第一个Linear的\(C_{in}\)和\(C_{out}\)分别为\(C\)和\(3\cdot C\);第二个Linear是通道数为\(C\)的全连接层
- 在具体实现中,经过第一个Linear后会首先reshape到\(B\cdot n\times wH\cdot wW\times 3 \times h\times \frac{C}{h}\),再permute为\(3\times B\cdot n\times h\times wH\cdot wW\times \frac{C}{h}\),并分到\(q,k,v\),它们的尺寸即为\(B\cdot n\times h\times wH\cdot wW\times \frac{C}{h}\)
- scale即传统attention机制中的\(\frac{1}{\sqrt{d}}\),可以手动指定,也可以使用\(\sqrt{\frac{C}{h}}\)
- RPB,即Relative Position Bias,下文详细介绍
- mask通过在对应位置加上
-infinite实现 - 与\(v\)矩阵点成后得到的尺寸为\(B\cdot n\times h\times wH\cdot wW\times \frac{C}{h}\),先
torch.transpose(1, 2)转置再reshape后尺寸为\(B\cdot n\times wH\cdot wW\times C\),最后送入第二个Linear中
总而言之,此处的attention最终公式为:
Mask操作
mask操作如下图所示,其中的mask可以根据偏移窗口时的偏移量预先得到,是固定的:
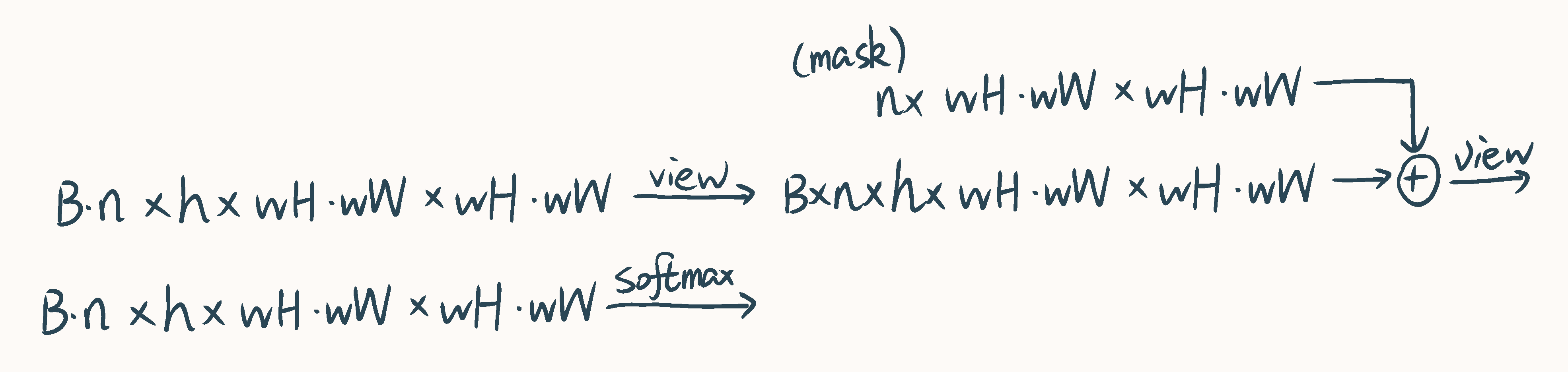
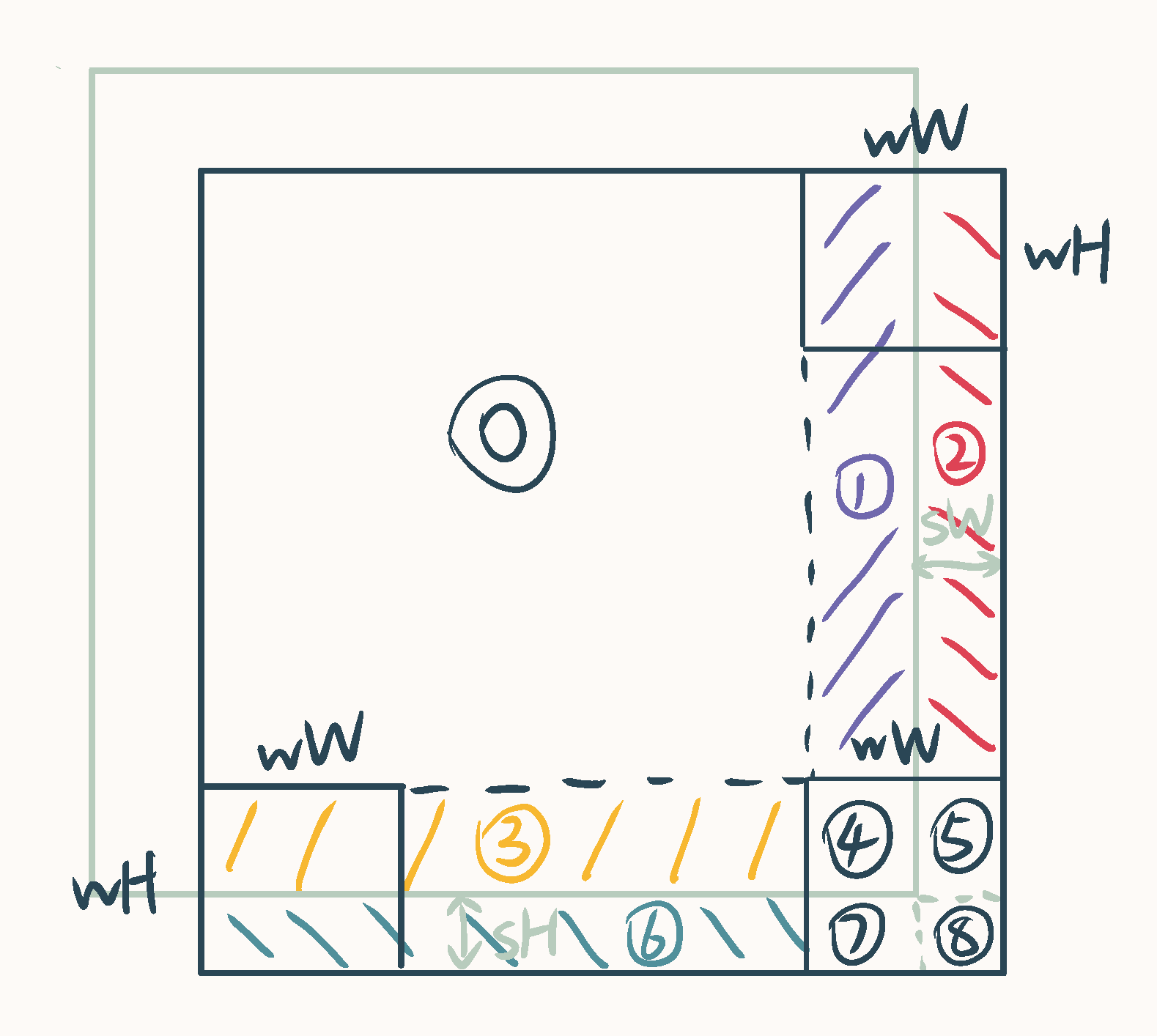
在具体实现中,原文所附代码采用上图所示分区方法,以矩形为单位给对应区域赋上编号,可作差后非零处即为需要mask的地方。上图中浅色框表示原特征图,深色框表示循环偏移后的特征图,由于约定了偏移量必须小于窗口大小,只有最边缘的窗口涉及mask操作。
Relative Position Bias
RPB为每两个窗口准备了一个可训练的参数值,用以表示这两个参数之间的“相对位置”量。任两个窗口之间纵向、横向的相对位置范围(0-index)为\([-wH+1,wH-1]\)、\([-wW+1,wW-1]\),因此参数表中的参数数量应为\((2wH-1)\cdot (2wW-1)\cdot h\)。
原文所附的代码实现中,使用了一个一维的参数表,并用另一个索引表完成相对位置坐标到参数表参数位置的映射。索引表position_index的尺寸为\(wH\cdot wW\times wH\cdot wW\),position_index[i][j]表示以i号窗口为参照时,j号窗口相对位置的参数位置值(窗口号按行主序计算,从左到右从上到下),记为\(a\),则还原为相对位置坐标后结果为: