编译技术（2）-上下文无关文法和分析

第2章 上下文无关文法和分析

基本概念

1. 可以将语法规则迭代地定义，直到每个元素都十分清楚，无需进一步描述

2. 字母表：基本的、不可再分（可以理解为够清楚无需再分）的元素的集合，常用符号\(\Sigma\)表示

   下面是一些字母表的例子： 英文字母表：\(\left\{a,b,\dots,z,A,B,\dots,Z\right\}\)

   社会主义核心价值观：\(\left\{富强,民主,文明,和谐,自由,平等,公正,法治,爱国,敬业,诚信,友善\right\}\)

3. 文法：用于定义刻画语法规则，用文法可以准确地判断某符号串是否符合语法规则的定义

4. 语言：某个字母表上任意数量（也就是可以无数个）的符号串的集合（显然字母表本身也是一个语言）

符号串及其运算表示

符号串，即一个字母表中的若干符号构成的一个有序序列。空串是不包含任何符号的特殊串，用\(\varepsilon\)表示。定义\(\varepsilon x=x\varepsilon=x\)

下面是符号串的两种运算

1. 符号串\(w\)的长度表示为\(|w|\)
2. 符号串的连接运算：设符号串\(x=a_1a_2\)、\(y=b_1b_2\)，则这两个符号串的连接\(xy=a_1a_2b_1b_2\)
3. 符号串的前缀、后缀和子串：对于任意\(w,x,y,z\in\Sigma^*\)，若\(w=xyz\)，则\(x\)为\(w\)的前缀、\(y\)为\(w\)的中缀、\(z\)为\(w\)的后缀。显然，前缀、后缀和子串都是从原符号串中截取的连续的一段（当然也包括\(\varepsilon\)）

下面是语言的6种运算，设下面的\(L\)和\(M\)是两个语言

1. 语言的并运算：\(L\cup M=\left\{s|s\in L或s\in M\right\}\)
2. 语言的连接运算：\(LM=\left\{ab|a\in L,b\in M\right\}\)
3. 语言的0次幂：\(L^0=\left\{\varepsilon\right\}\)
4. 语言的n次幂：\(L^n=LL^{n-1}=L^{n-1}L,n\ge1\)
5. 语言的*闭包：\(L^*=L^0\cup L^1\cup L^2\cup \dots\)
6. 语言的+闭包：\(L^*=L^1\cup L^2\cup \dots\)

文法

基本概念

一个文法可以由终结符集合\(V_T\)、非终结符集合\(V_N\)、开始符号\(S\)、产生式集合\(P\)来定义，即\(G[S]=(V_T,V_N,S,P)\)

终结符，即组成符号串的基本符号（无需再分）；开始符号能表示出的所有符号串的集合就是此文法所定义的语言

产生式以\(A\rightarrow\alpha\)的形式出现:\(A\in V_N\)、称为产生式的左部，\(\alpha\in (V_T\cup V_N)^*\)、称为产生式的右部

下面是一个产生式集合的例子：

事实上，具有相同左部的产生式可以合并，合并后的各个右部称为候选式，例如上面的产生式集合就可以合并为

推导和归约

推导和归约可以帮助我们根据文法分析给定的输入串是否符合文法定义的规则。推导，即用产生式的右部替换左部（将左部变为右部）；归约，即用产生式的左部替换右部（将右部变为左部）。显然，推导和归约可以连续地进行，可以进行一步，也可进行n步，一步推导/一步归约也称为直接推导/直接归约

推导的步数可以写在推导箭头符号的上方，特别的，\(\overset{+}{\Rightarrow}\)表示1步或多步推导、\(\overset{*}{\Rightarrow}\)表示0步或多步推导

对于上面举例的产生式集合，下面是一对互逆的推导和归约

最左推导，即最右归约，指的是每一步都选择最左边的非终结符进行替换；最右推导，即最左归约，指的是每一步都选择最右边的非终结符进行替换；规范归约，即最左归约；规范推导，即最右推导

文法定义的语言

对于某一文法\(G[S]\)，进行如下定义

1. 句型：从开始符号出发推导得到的序列
2. 句子：仅包含终结符的句型
3. 该文法定义的语言：从该文法中可以得到的所有句子的集合，表示为\(L(G[S])=\left\{w|w\in V_T^*\wedge S\overset{*}\Rightarrow w\right\}\)

当文法定义的语言是相同的，则称这些文法是等价的

:star: 考察点：语言和文法的互相转化

根据文法写出语言较为简单，写几个找找规律一般就可以总结出来文法对应的语言；而要将语言对应到某种文法上则较为困难，下面是几种典型的语言结构

1. 重复构造

   可以使用递归定义简单实现

   \(\left\{(a)^n|n\ge 1\right\}\)：

   $$ S\rightarrow aA\\ A\rightarrow aA|\varepsilon $$

   \(\left\{(ab)^n|n\ge 0\right\}\)：

   $$ S\rightarrow abS|\varepsilon $$

2. 基本元素的任意组合

   对各基本元素进行递归定义即可实现

   \(\left\{a,b\right\}^*\)：

   $$ S\rightarrow aS|bS|\varepsilon $$

3. 顺序结构

   构成整个有序的每个小模块分别按照第一种重复构造的方法递归定义

   \(\left\{a^nb^m|n\ge 0,m\ge0\right\}\)：

   $$ S\rightarrow AB\\ A\rightarrow aA|\varepsilon\\ B\rightarrow bB|\varepsilon $$

   \(\left\{a^nb^m|n\ge 0,m\ge1\right\}\)：

   $$ S\rightarrow AB\\ A\rightarrow aA|\varepsilon\\ B\rightarrow bY\\ Y\rightarrow bY|\varepsilon $$

4. 对称结构

   往往会把终结符放在两侧，将非终结符夹在中间，以反映“对称”

   \(\left\{a^nb^n|n\ge 0\right\}\)：

   $$ S\rightarrow aSb|\varepsilon $$

   \(\left\{a^nb^n|n\ge 1\right\}\)：

   $$ S\rightarrow aAb\\ A\rightarrow aAb|\varepsilon $$

   \(\left\{a^ncb^n|n\ge 0\right\}\)：

   $$ S\rightarrow aSb|c $$

文法的种类

0型文法

也称为短语文法，由0型文法定义的语言称为0型语言或递归枚举语言。

对产生式集合的要求

• 其中所有产生式的左部都至少包含一个非终结符

对任意\(\alpha\rightarrow\beta\in P\)，若\(\alpha,\beta\in (V_N\cup V_T)^*\)，且\(\alpha\)中至少包含一个非终结符

1型文法

也称为上下文相关文法，由1型文法定义的语言称为1型语言或上下文相关语言

对产生式集合的要求

• 所有产生式左部长度不大于右部长度（除了\(S\rightarrow\varepsilon\)）
• S不能出现在任何产生式的右部

2型文法

也称为上下文无关文法，由2型文法定义的语言称为2型语言或上下文无关语言

对产生式集合的要求

• 所有产生式左部必须为一个非终结符

3型文法

也称为正则文法、正规文法，包括左线性文法和右线性文法，由3型文法定义的语言称为3型语言、正则语言或正规语言。

对产生式集合的要求

• 所有产生式左部必须为一个非终结符
• 所有产生式右部只有三种选择：一个终结符与一个非终结符的连接、终结符、\(\varepsilon\)（或一个非终结符与一个终结符的连接、终结符、\(\varepsilon\)）

语法树

对于某文法，语法树的定义如下：

1. 语法树是一棵有序树，即兄弟结点位置不能交换
2. 每个内部结点（即非叶子结点）都是一个非终结符
3. 树根是开始符号S
4. 每个叶子结点属于\(V_N\cup V_T\cup \left\{\varepsilon\right\}\)，但当叶子结点是\(\varepsilon\)时，它必须是其父结点的唯一孩子
5. 对任意一个内部结点A，设其孩子从左到右分别为\(X_1,X_2,\dots,X_k\)，则\(A\rightarrow X_1X_2\dots X_k\in P\)

一个语法树对应着该文法的一个句型，同时也表现了根据该文法的产生式推导（从上到下）或归约（从下到上）出这个句型的过程。下面是一个例子（以最左推导为例）

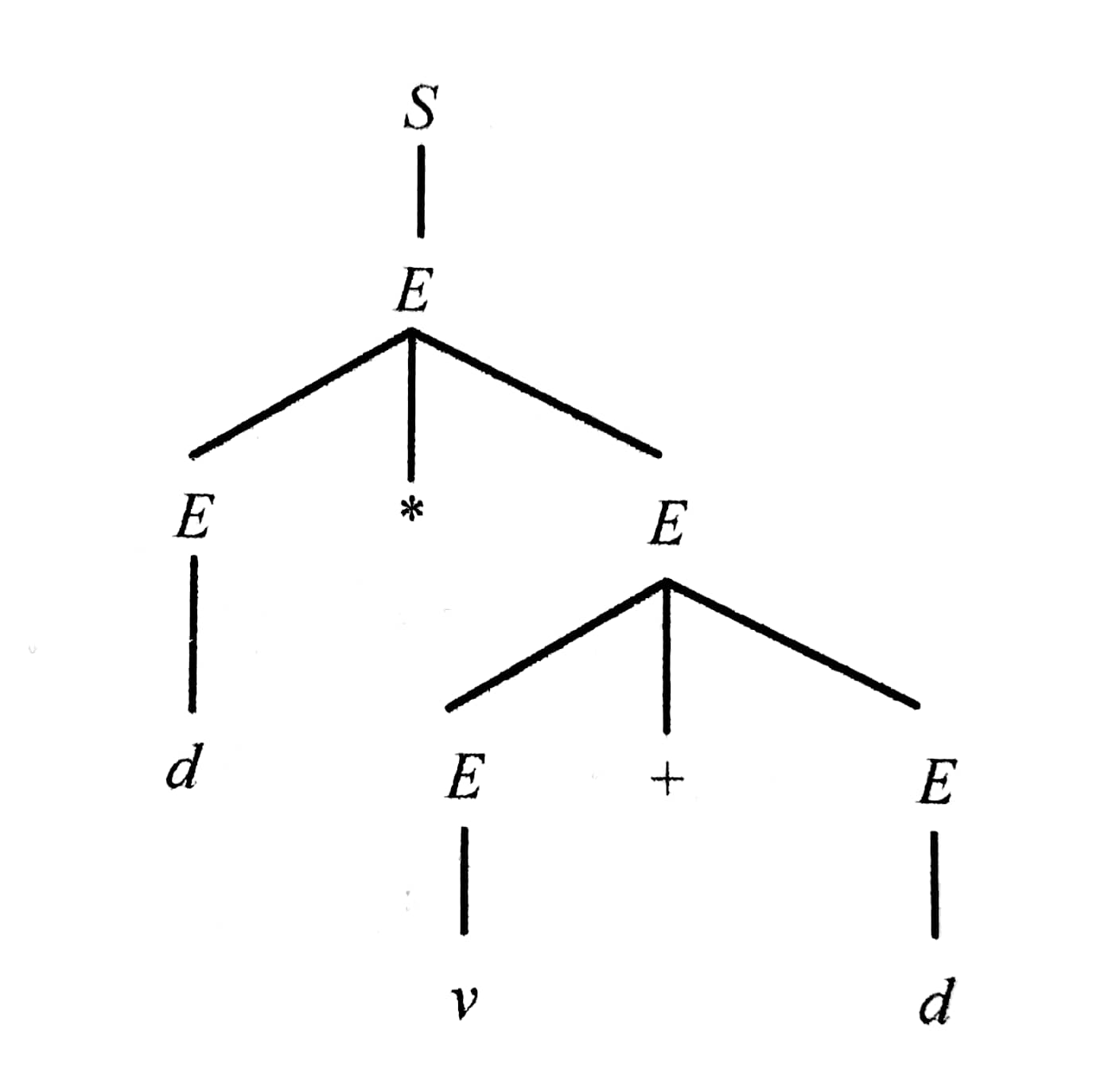
若对于某个文法，一个句型的语法树不是唯一的，也就代表对于同一句型可以有不同的推导顺序，则这个文法是二义的

短语和句柄相关概念

语法树中有一些特殊的概念

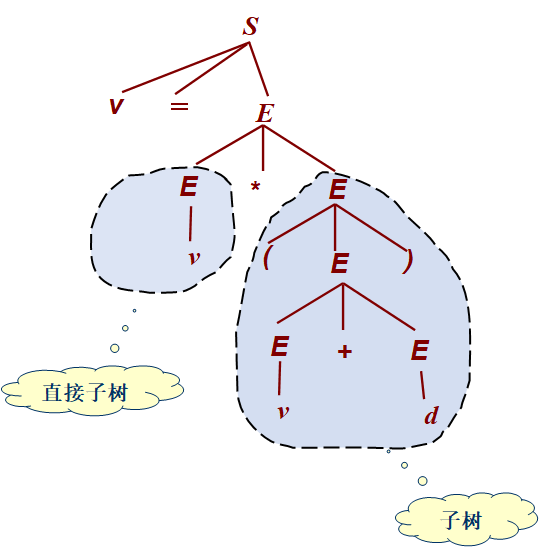
1. 子树：以一个内部结点为根结点的树（包括这个内部结点）
2. 直接子树：只有一个内部结点的子树
3. 短语：子树的所有叶子结点从左到右组成的串
4. 直接短语：直接子树的所有叶子结点从左到右组成的串
5. 句柄：整个语法树中最左边的直接短语

:star: 考察点：找语法树中的短语、直接短语、句柄

此处以例子进行说明。下图中的语法树共有3个直接子树、7个子树，句柄为\(v\)（即标出的直接子树中的那个\(v\)）。标出的直接子树对应的直接短语为\(v\)、标出的子树的短语为\((v+d)\)