编译技术（4）-语义分析

第4章 语义分析

显然，单纯使用语法分析，只能判断词法记号的出现位置是否正确，无法判断所有的语言规则，也就是说，只使用上下文无关文法是无法完整描述一个语言的所有规则的。

语义分析要完成的任务就是：在语法分析的基础上，计算程序的辅助信息。可以认为语义分析是一种上下文相关的分析。

对于程序中出现的各种名字（例如变量、常量、函数、记录等），编译器需要知道他们的相关特征，这些特征称为对应名字的属性

常见语义约束

作用域检查

主要包括重复声明和强制声明的检查

类型检查

类型检查会计算所有语言实体的类型属性，并判断它们在上下文中是否符合语言的类型约束，主要针对表达式和语句

除了上面两种语义约束外，还有唯一性约束（例如对于枚举类型只能定义一次）、控制流约束（例如分支语句的完整性）等

属性文法

基本概念与定义

文法符号\(X\)的属性\(a\)表示为\(X.a\)，属性可以具体指名字、数据类型、值等

每个产生式可以对应0个或多个语义规则，每一个语义规则都是其对应产生式上的一个静态约束。另外，对于产生式中多次出现的符号，为了能够正确地在语义规则中进行表示，会加下标作为区分的标志

属性文法定义

属性文法定义在上下文无关文法的基础之上，通过文法符号的属性及其计算规则增加了相关的约束。若对于每个规则，不仅使用其他属性值或常量来定义一个属性，这样的属性文法称为语法制导定义

语义规则定义

对于产生式\(A\rightarrow\alpha\)，其语义规则为\(b=f(c_1,c_2,\dots,c_k)\)，其中\(b,c_1,c_2,\dots,c_k\)为该产生式中文法符号的属性，而\(f\)是一个函数

综合属性与继承属性

在上述语义规则的定义中： - 若\(b\)是\(A\)的一个属性，且\(c_1,c_2,\dots,c_k\)均为产生式右部文法符号的属性或者\(A\)的其他属性，则称\(b\)是\(A\)的综合属性（下到上传播） - 若\(b\)是产生式右部某个文法符号\(X\)的一个属性，且\(c_1,c_2,\dots,c_k\)均为产生式右部文法符号的属性或者\(A\)的属性，则称\(b\)是\(X\)的继承属性（上到下传播）

一般情况下，在实际判断综合属性和继承属性时，只要看语义规则等号左边的属性即可。若该属性是对应产生式左部的，则为综合属性；若该属性是对应产生式右部的，则为继承属性

注释语法树

即表示出每个符号属性值的语法树

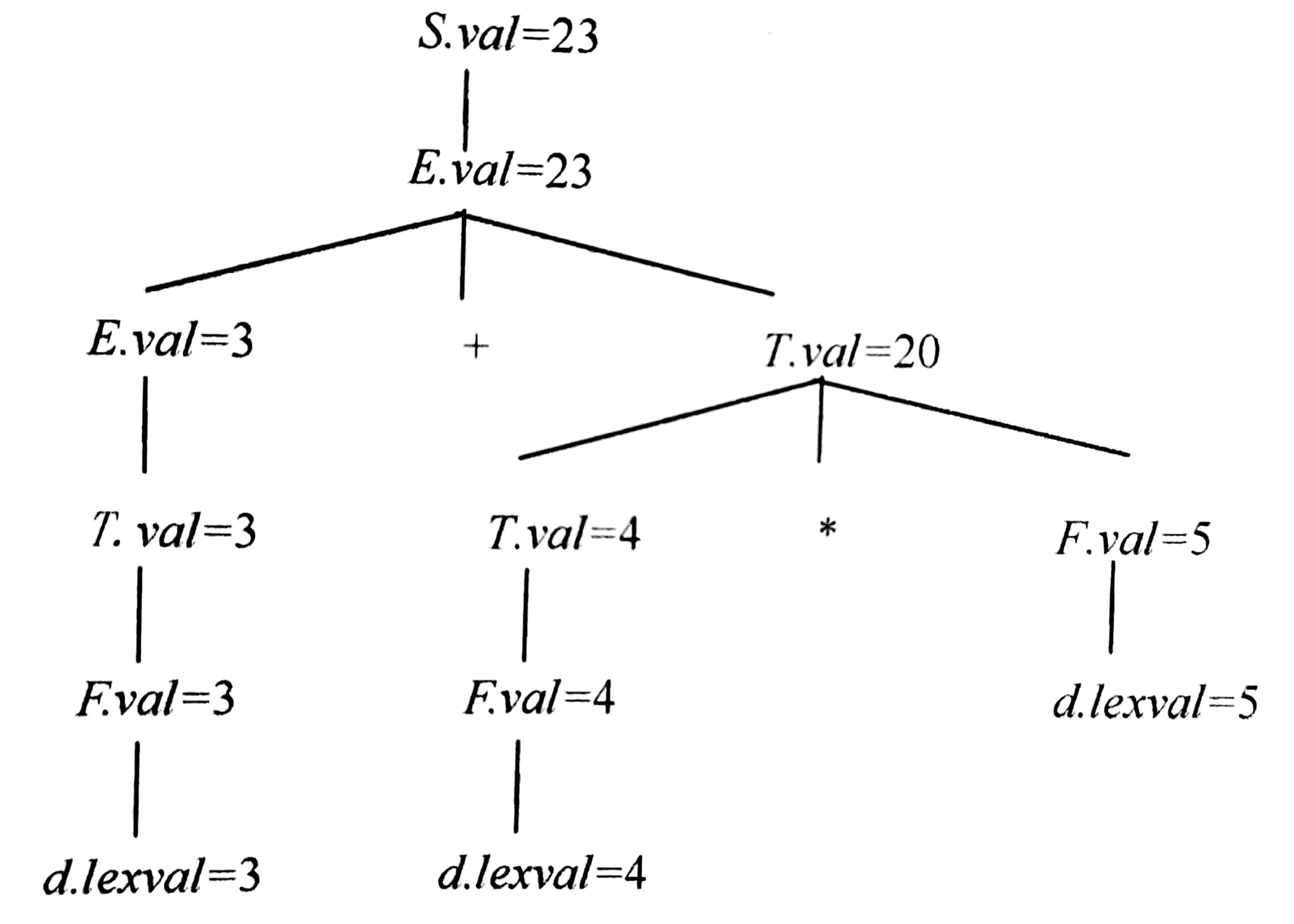
语法制导定义

很多情况下，除了用其他属性值或常量定义一个属性之外，还需要对属性做一些其他的操作，甚至是根据属性对编译过程中所需的一些东西进行处理（例如登记到符号表中，这种语义动作可以视为综合属性）

例如上面的第一条语义规则就是对\(E.val\)进行输出

属性计算

依赖图

依赖图是一个有向图，描述了语法树中结点的属性以及属性间的相互依赖关系

下面从一个例子入手，说明依赖图的画法

此处以语句x,y:integer为例（x, y均为标识符id）

Step 1：在语法树上添加相关属性

对于语法树上的每个结点，在旁边写上其相关的属性或者操作

Step 2：在属性间添加依赖

根据语法树推导使用到的产生式画有向边，有向边从被依赖的属性出发。例如对于产生式\(D\rightarrow L:T\)的语义规则\(L.in=T.type\)，有向边从\(T.type\)指向\(L.in\)

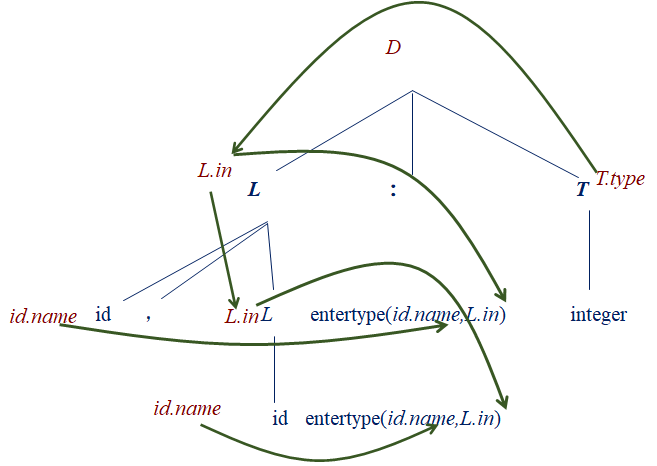
显然，在得到属性间的所有依赖关系之后，为了正确成功计算出所有属性，只要找出所有属性的一个拓扑排序并据此顺序计算属性即可

综上，基于依赖图求取属性计算顺序是一种多遍组织的分析方法： - 构造语法树 - 构造依赖图 - 拓扑排序，若无圈则得到一个计算顺序

L属性和S属性的语法制导定义

事实上，若随便给一个语法制导定义，很可能存在循环依赖或是不存在一个可以顺利求出所有属性的求值顺序

因此，定义一种一定存在一个从左到右计算顺序的特殊的语法制导定义，称为L属性定义，在L属性定义中，对于任何一个产生式\(A\rightarrow X_1X_2\cdots X_n\)（\(X_i\)为文法符号），其涉及到的每个属性都满足下面任一条：

1. 若它是\(X_i(i=1,2,\dots,n)\)的继承属性，则该属性只依赖于\(A\)（即父结点）的继承属性或\(X_1X_2\cdots X_{i-1}\)（即左边已经算过的兄弟节点）的属性
2. 该属性是综合属性

更特殊地，若L属性定义中只有综合属性，则称之为R属性定义，直接按语法树的后序遍历顺序就可以求出所有属性

这里以下面的语法制导定义为例，判定其是否是L属性定义

Step 1：判断属性类型

• 综合属性：\(A.s,B.s\)
• 继承属性：\(A.i\)

Step 2：逐个看产生式

第一个产生式涉及属性\(A.i,B.s\)： - \(B.s\)是综合属性……OK - \(A.i\)依赖\(B.s\)，而\(B\)不在\(A\)的左边……FAILED

因此，这个语法制导定义不是L属性定义

语法制导翻译

语法制导翻译，即将语义分析结合到语法分析中进行，可以一遍完成

所有L属性的语法制导定义都可以一遍完成语法分析与语义分析，即存在一个和语法分析顺序相同的属性计算顺序

翻译模式

将语义规则中包含的程序片段用花括号{}括起来，称为语义动作，将这些语义动作放到生成式的合适位置上，就可以得到属性文法对应的翻译模式

需要注意的是，在翻译模式中，必须确保每个属性在被访问时存在且已经求值

如此，对于计算综合属性的语义规则，将语义动作放在对应产生式的尾部即可；而对于计算继承属性的语义规则，将语义动作放在该属性所属非终结符的前面

在上图的例子中，只有\(R.i\)是继承属性。因此在产生式\(L\rightarrow SR\)中将计算它的语义动作\(\{R.i=S.num\}\)放在非终结符\(R\)的前面；在产生式\(R\rightarrow ,SR_1\)中将计算它的语义动作\(\{R_1.i=R.i+S.num\}\)放在非终结符\(R_1\)的前面

嵌入语义动作的语法树

对于一个L属性的语法制导定义，可以将语义动作嵌入到其某个句型的语法树中。按照从左到右的深度优先遍历就可以直接得到每一个语义动作的执行时机

需要注意的是，对于多次出现的同一个非终结符，为了便于表达，会使用下标加以区分

下面是句型(a,(a))的语法树嵌入了语义动作之后的结果，使用的就是上述作为例子的翻译模式

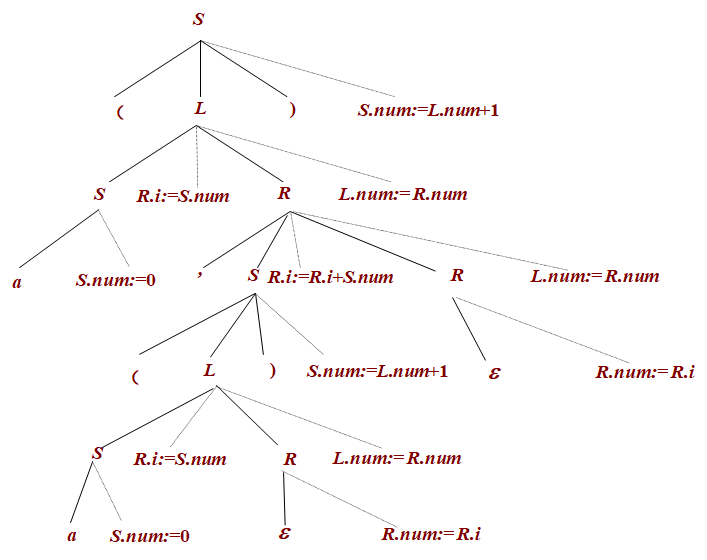
在递归下降分析程序中加入语义分析

对于L属性的语法制导定义来说，只要得到了翻译模式，可以非常简单地将之前用于语法分析的递归下降分析程序修改为附带了语义分析的递归下降分析程序

关键点：在前序遍历中计算继承属性，在后序遍历中计算综合属性；继承属性采用参数实现，综合属性采用函数返回值实现。若要返回的综合属性有多个，可以考虑返回结构体

需要修改的地方： 1. 为每个非终结符定义的函数，要以其继承属性为形参，并将其综合属性作为返回值 2. 在调用非终结符的解析函数时，需要传入对应的参数并接收其返回值

根据上面作为举例的翻译模式可以写出如下递归下降分析程序（附带语义分析）的代码，此处省略了FIRST和FOLLOW集的计算，直接给出程序

/*
    S→(L){S.num=L.num+1}
    S→a{S.num=0}
*/
// S有综合属性S.num，没有继承属性
int parseS() {
    if (token == '(') {
        gettoken();
        Lnum = ParseL();
        if (token == ')') {
            gettoken();
            Snum = Lnum + 1;
        } else error();
    } else if (token == 'a') {
        Snum = 0;
    } else error();

    // 返回综合属性
    return Snum;
}

/*
    L→S{R.i=S.num}R{L.num=R.num}
*/
// L有综合属性L.num，没有继承属性
int parseL() {
    if (token == '(' || token == 'a') { // FIRST(S)
        Snum = parseS();
        Ri = Snum;
        // 传入继承属性
        Rnum = parseR(Ri);
        Lnum = Rnum;
    } else error();

    // 返回综合属性
    return Lnum
}

/*
    R→,S{R1.i=R.i+S.num}R1{R.num=R1.num}
    R→ε{R.num=R.i}
*/
// R有综合属性R.num，有继承属性R.i
int parseR(int Ri) {
    if (token == ',') {
        gettoken();
        Snum = parseS();
        R1i = Ri + Snum;
        // 传入继承属性
        R1num = parseR(R1i);
        Rnum = R1num;
    } else if (token == ')') { // FOLLOW(R)
        Rnum = Ri;
    } else error();

    // 返回综合属性
    return Rnum
}

符号表

代码中势必会有各种类型各种名字的变量，在编译过程中，将这些信息记录在符号表中，并借此完成变量存储地址规划、变量类型检查等工作。

符号表中要记录的内容

名字、类型、地址

显然，符号表中记录的其实就是各个变量的名字及其各种属性，一般来说，符号的名字、类型、地址是必须要记录的。由于名字往往是不定长的，符号表中保存指针即可。

内情向量

例如对于数组来说，除了上面三个基本信息外，还需要记录数组的维数、每一维的上下界等信息。一般来说，会设一个内情向量指针的字段，指向记录了这些信息的内情向量。

形参

可以用链表的结构将函数的形参串在一起，符号表中对应的字段称为形参域

嵌套作用域管理

在不同的作用域中，可以定义相同名字的符号。一般来说，为了实现嵌套作用域的管理，符号表的实现有两种方式：

• 每一个作用域单独有一个符号表
• 所有作用域共用一个符号表，在符号表中添加作用域号（层次号）

此处引进开作用域的概念，程序中某一个点的开作用域就是该点所在的作用域以及包含它的程序单元所构成的作用域。若某一符号在多个开作用域中被声明，则将最近的声明视为该符号的声明。

下面的动图展示了所有作用域共用一个符号表的情况

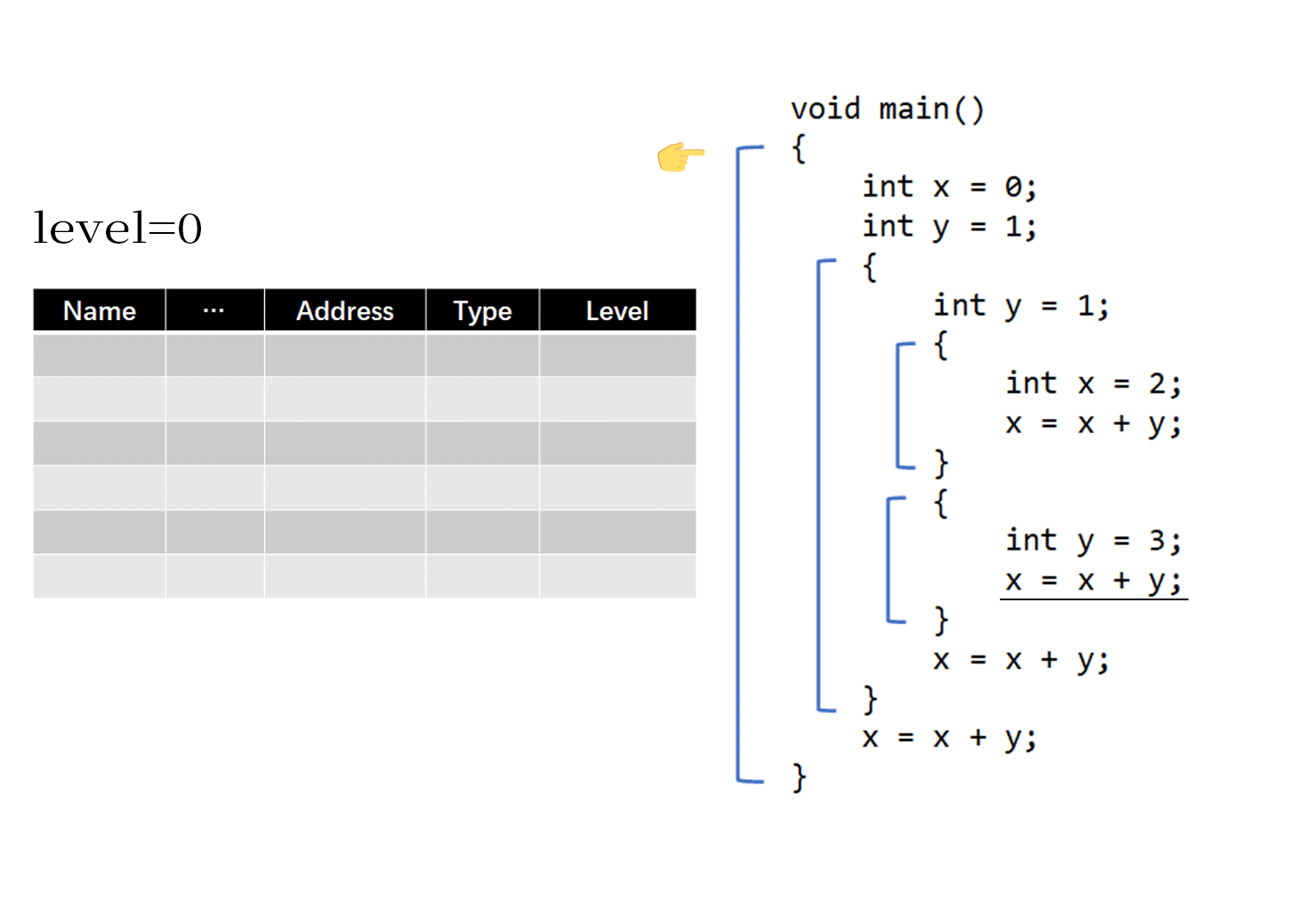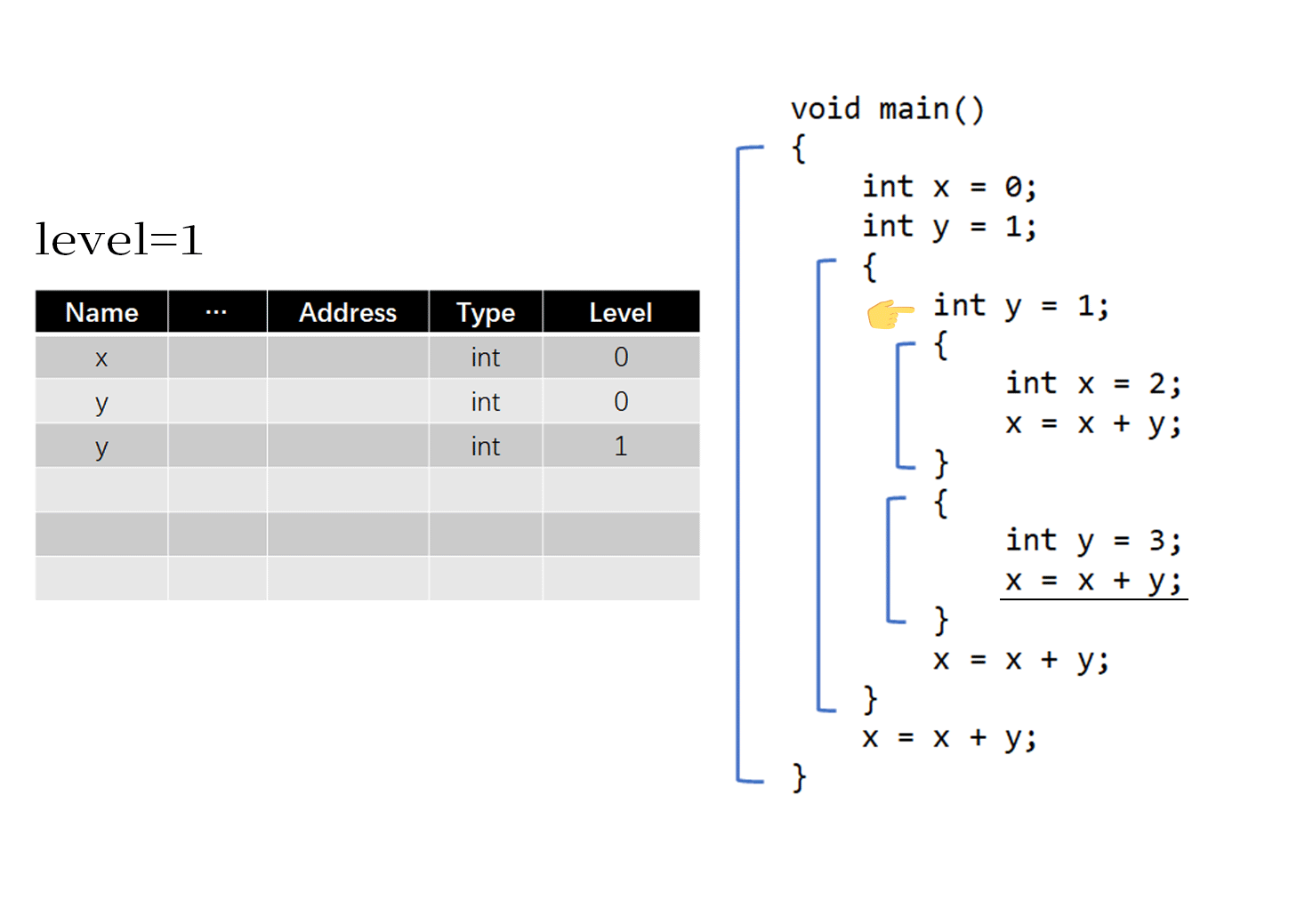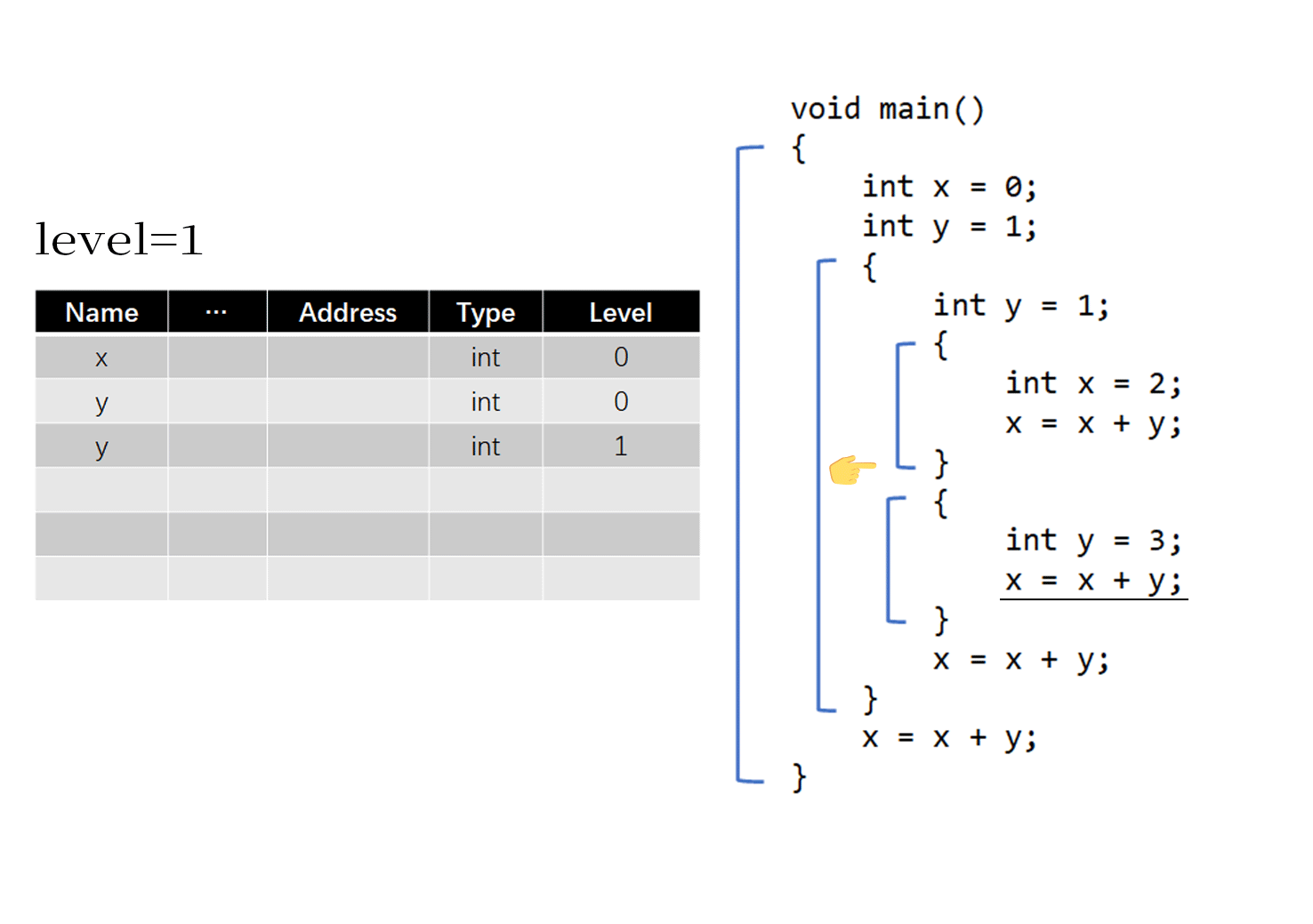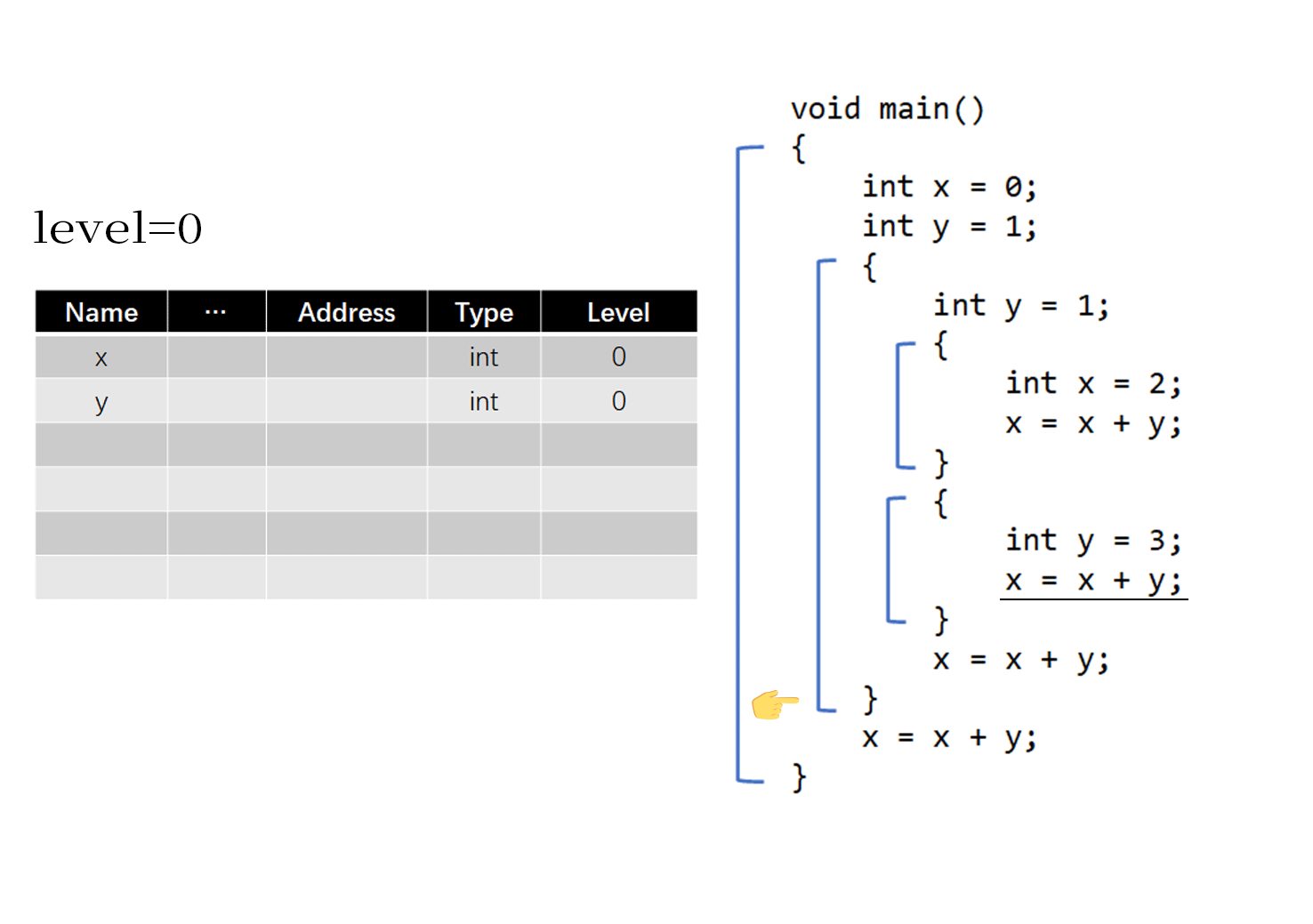
对于上面的GIF示意图，需要注意以下几点：

1. 在脱离出一个作用域时，应该删除该作用域中相关的符号，并将level标记值减一
2. 在进入一个作用域时，要将level标记值加一
3. 在搜索某一符号时，从后往前按序寻找即可

例如在执行横线划出的x=x+y时，从下往上查符号表，会找到处于level=2的、值为3的y以及level=0、值为0的x

类型检查

类型检查的作用在于确保代码的每一个部分都是有意义的，将一些语义动作添加到翻译模式中就可以完成类型检查的工作。

在翻译模式的设计中，关键点在于每个“表达式”其实都有一个类型属性，通过继承属性和综合属性传递推导中得到的类型属性，判断是否一致。

在类型检查的过程中，根据语言的设计，还可以完成类型隐形转换的工作。

对于最终可以解析得到符号类型的产生式，可直接得到类型，例如E→true {E.type=bool}；对于存在进一步推导的，可以通过综合属性得到本产生式的类型，例如S→if E then S1 {S.type=S1.type if E.type=bool else type_error }