georgehu学习生活 - 论文阅读-Zero-shot Scene Graph Generation via Triplet Calibration and Reduction

TOMM 原文链接：Zero-shot Scene Graph Generation via Triplet Calibration and Reduction

基本介绍

场景图生成（SGG）任务：从图片中提取目标之间的关系，并以结构化的图表示，最常见的就是通过主谓宾这样的三元组来结构化地描述场景中各目标之间的关系。zero-shot SGG指的就是训练时看过某个主体，看过某个客体，也看过某种谓词关系，但没有看过这三个组合起来的三元组，在测试时要求识别出这种没看过的三元组。下图直观地展示了上述任务

零样本场景图生成任务示意图

主要贡献：

提出了Triplet Calibration Loss，用以平衡对未见三元组的约束，使其不会被错误地标为背景，还可以加强出现较少三元组类别的attention
提出了Unseen Space Reduction Loss，用以削减本来巨大的未见三元组空间，使模型聚焦于合理的未见三元组组合
使用了Contextual Encoding Network来编码相对空间特征

整体模型框架图如下：

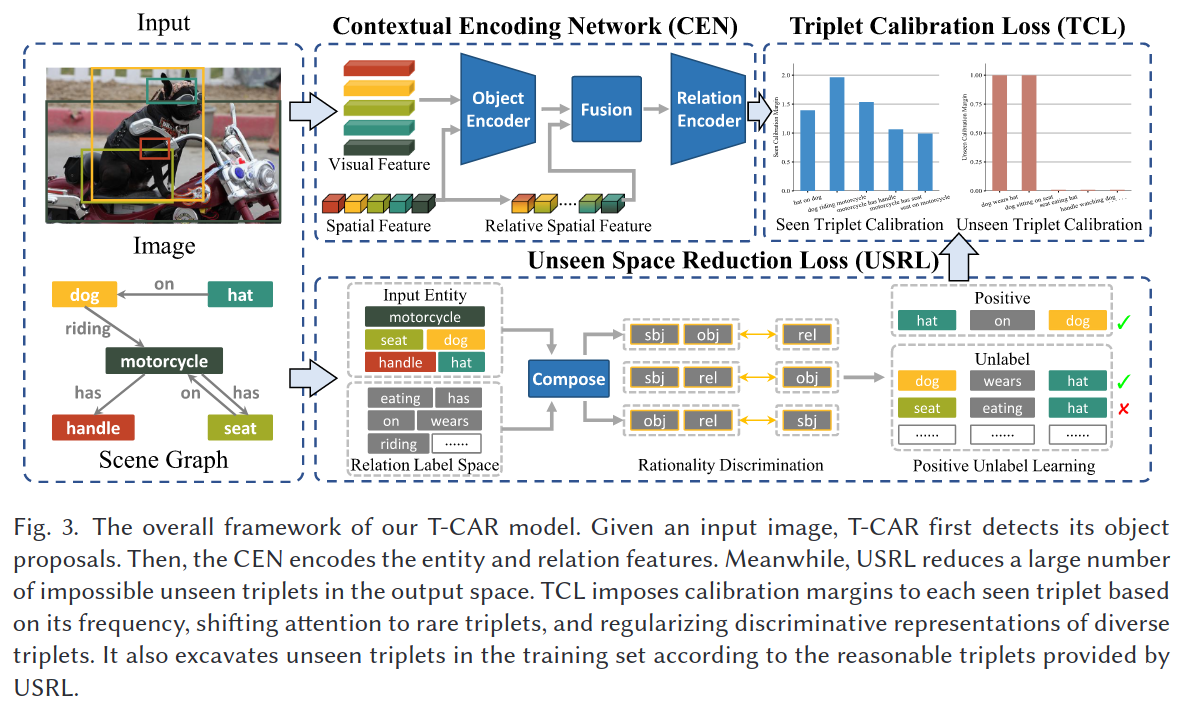
T-CAR模型总框架图

Contextual Encoding Network

在SGG任务中，实体（主体和客体）的特征表示一般由视觉和对应标签的语言学特征（例如Word2Vec）组成；关系则由视觉和主客体的空间特征组成。显然，语言学特征会带来一些先验的偏差；而简单的结合主体和客体各自的空间特征显然也是不利于对于未见三元组的挖掘的。

使用CEN就可以避免使用语言学特征，从而免于受到先验偏差的影响，并且其中还显式地建模了主客体的相对空间特征。CEN由entity encoder, fusion layer与relation encoder组成。

Object Encoder

$$ \left\{ x_i \right\}_{i=1,\dots,N} = \text{Enc}_{obj}\left(\left\{\left[v_i,\text{FFN}\left(b_i\right)\right]\right\}_{i=1,\dots,N}\right) $$

其中 $N$ 为实体的数量， $x_i$ 为精炼后的实体表示， $v_i$ 为视觉特征， $b_i$ 为实体的bounding box，FFN用的是一个两层的MLP（激活函数为LeakyReLU）, $\text{Enc}_{obj}$ 为客体上下文编码模块，可以选用多层LSTM、GNN或是Transformer，本文使用了一个四层的Transformer。公式中的中括号表示concat操作，并且是在最后一维上进行拼接。

Fusion Layer

$$ x_p' = x_s \star x_o \star \text{FFN}\left(\left[v_u, b_{s,o}\right]\right) $$

其中 $x_p'$ 为初始谓词表示，计算时用到了entity encoder中得到的精炼实体表示， $x_s$ 与 $x_o$ 为当前关系对应的主体和客体， $v_u$ 表示主体 $s$ 与客体 $o$ 的联合框（union box）部分的视觉特征， $b_{s,o}$ 为主客体间的相对空间特征。 $\star$ 的计算规则如下，其中的 $W_x$ 与 $W_y$ 为投影矩阵：

$$ x \star y = \text{ReLU}\left(W_x x + W_y y\right) - \left(W_x x - W_y y\right) \odot \left(W_x x - W_y y\right) $$

联合框（union box）指的是同时包含需要内容的最小矩形框

相对空间特征由 $b_{ul}$ （union box location）、 $b_{sl}$ （size-related location）与 $b_{rl}$ （relative location）concat而成，即 $b_{s,o}=\left[b_{ul},b_{sl},b_{rl}\right]$ ，这三个部分的计算如下：

$$ b_{ul} = \left( \frac{x_u^1}{w}, \frac{y_u^1}{h}, \frac{x_u^2}{w}, \frac{y_u^2}{h}, \frac{x_u^1 + x_u^2}{2w}, \frac{y_u^1 + y_u^2}{2h}, \frac{w_u}{w}, \frac{h_u}{h} \right) $$

$$ b_{sl} = \left( \log \left( \frac{w_s}{w_o} \right), \log \left( \frac{h_s}{h_o} \right), \log \left( \frac{w_o}{w_s} \right), \log \left( \frac{h_o}{h_s} \right) \right) $$

$$ b_{rl} = \left( \frac{x_s^1 - x_o^1}{w_o}, \frac{y_s^1 - y_o^1}{h_o}, \frac{x_s^2 - x_o^2}{w_o}, \frac{y_s^2 - y_o^2}{h_o}, \frac{x_o^1 - x_s^1}{w_s}, \frac{y_o^1 - y_s^1}{h_s}, \frac{x_o^2 - x_s^2}{w_s}, \frac{y_o^2 - y_s^2}{h_s} \right) $$

其中 $\left(x^1,y^1\right)$ 与 $\left(x^2,y^2\right)$ 表示对应bounding box两个角的坐标，例如主体bbox就可以表示为 $b_s=\left(x_s^1,y_s^1,x_s^2,y_s^2\right)$ ，客体的可以表示为 $b_o=\left(x_o^1,y_o^1,x_o^2,y_o^2\right)$ ； $\left(w,h\right)$ , $\left(w_s,h_s\right)$ 与 $\left(w_o,h_o\right)$ 则分别表示整个图片、主体部分和客体部分的宽高。

Relation Encoder

通过relation encoder，可以获得谓词的精炼特征 $z_j$ ：

$$ \left\{ z_j \right\}_{j=1,\ldots,N \times (N-1)} = \text{Enc}_{rel}\left(\left\{ x_j' \right\}_{j=1,\ldots,N \times (N-1)}\right) $$

其中的 $\text{Enc}_{rel}$ 关系上下文提取模块，本文使用了个两层的Transformer。

最后使用全连接层分别得到预测客体类别和谓词类别的logits， $e_i$ 和 $r_j$ ：

$$ e_i=\text{FC}_{obj}\left(x_i\right)\\ r_j=\text{FC}_{rel}\left(z_j\right) $$

Triplet Calibration Loss

Unseen Triplet Calibration

由于可见三元组类别占据统治地位，这会大大压缩未见类别的预测概率，即模型给出的预测会偏向于出现频率较高的类别。由此，在未见三元组类别上引入一个矫正损失 $\mathcal{L}_{cal}$ ，使得未见三元组类别的logits不至于太小，其中的 $C_{tpt}^u$ 为未见三元组集合， $r_{s,o}^c$ 为主体 $s$ 与客体 $o$ 间关系编码在第c类关系上的logits， $C_p$ 为所有关系类别的集合：

$$ \mathcal{L}_{cal}(r_{s,o}) = -\log \left( \sum_{(s,c,o) \in C_{tpt}^u} \frac{\exp(r_{s,o}^c)}{\sum_{c' \in C_p} \exp(r_{s,o}^{c'})} \right) $$

同时，为了防止未见三元组的概率过大导致已见三元组的概率受到影响，设计一个硬边界来约束 $\mathcal{L}_{cal}$ ：

$$ \begin{aligned} \mathcal{L}_{cal}^m(r_{s,o}) &= \mathcal{L}_{cal}(r_{s,o} + \mathbb{I}_m(s, :, o))\\ &= -\log \left( \sum_{(s,c,o) \in C_{tpt}^u} \frac{\exp(r_{s,o}^c + 1)}{\sum_{c' \in C_{tpt}^s} \exp(r_{s,o}^{c'} - 1) + \sum_{c'' \in C_{tpt}^u} \exp(r_{s,o}^{c''} + 1)} \right) \end{aligned} $$

其中的 $C_{tpt}^s$ 为已见三元组集合， $\mathbb{I}_m(s, :, o)\in\mathbb{R}^{\left|C_p\right|}$ 称为边界向量，其中各元素的值计算如下

$$ \mathbb{I}_m(s, c, o)= \begin{cases} 1,\quad &(s,c,o)\in C_{tpt}^u\\ -1,\quad &(s,c,o)\in C_{tpt}^s \end{cases} $$

Seen Triplet Calibration

关系在不同的主客体上的分布是不一样的，很可能存在某些主客体的关系分布和整体数据集上的大相径庭，模型会更加倾向于出现频率更高的三元组，因此需要一个细粒度更细的方法来平衡这种倾向性。调整上述的硬边界为一个动态边界， $\mathcal{L}_{cal}^m(r_{s,o})$ 变为 $\mathcal{L}_{cal}^{m,\alpha}(r_{s,o})$ ，也就是说希望已见三元组中出现频率越高的约束越严格：

$$ \begin{aligned} \mathcal{L}_{cal}^m(r_{s,o}) &= \mathcal{L}_{cal}(r_{s,o} + \mathbb{I}_m^{\alpha}(s, :, o))\\ &= -\log \left( \sum_{(s,c,o) \in C_{tpt}^u} \frac{\exp(r_{s,o}^c + 1)}{\sum_{c' \in C_{tpt}^s} \exp(r_{s,o}^{c'} - \alpha_{s,c',o}) + \sum_{c'' \in C_{tpt}^u} \exp(r_{s,o}^{c''} + 1)} \right) \end{aligned} $$

即边界向量各元素的计算方式变为：

$$ \mathbb{I}_m^{\alpha}(s, c, o)= \begin{cases} 1,\quad &(s,c,o)\in C_{tpt}^u\\ \alpha_{s,c',o},\quad &(s,c,o)\in C_{tpt}^s \end{cases} $$

$$ \alpha_{s,c,o} = \log \left( \frac{n_{\text{max}}}{n_{s,c,o}} \right) \times \frac{\sum_{i \in C_{tpt}} n_i}{\sum_{j \in C_{tpt}} n_j \log \left( \frac{n_{max}}{n_j} \right)} $$

其中 $n_{max}$ 为出现次数最多的三元组的计数， $n_{s,c,o}$ 为三元组 $(s,c,o)$ 的计数，上面的 $\alpha_{s,c,o}$ 会随着 $n_{s,c,o}$ 的增加而减少。

同时，还将这种动态边界应用于CrossEntropyLoss：

$$ \mathcal{L}_{ce}^{m,\alpha}(r_{s,o}) = -\log \frac{\exp(r_{s,o}^c - \alpha_{s,c,o})}{\sum_{c'} \exp(r_{s,o}^{c'} - \alpha_{s,c',o})} $$

最终结合上述Unseen和Seen两种Triplet Calibration得到最终的Loss

$$ \mathcal{L}=\mathcal{L}_{ce}^{m,\alpha}+\lambda\mathcal{L}_{cal}^{m,\alpha} $$

另外，在推理时，会应用上硬边界来调整logits：

$$ predicate=\mathop{\text{argmax}}\limits_{c\in C_p}\left(r_{s,o}^c+\mathbb{I}_m\left(s,c,o\right)\right) $$

Unseen Space Reduction

之前SGG任务的解决方案中都会将所有未见的三元组搭配作为可能的三元组，但事实上有很多搭配并不符合实际，现实世界中不太可能存在，而有可能真实存在的三元组在所有搭配组合中仅占到了较小一部分。因此，减少未见三元组解空间可以使模型更好的找出未见三元组

下面的过程基于替换性假设：对于一个三元组，将其中的一个元替换为具有类似属性的内容后，该三元组依然有意义。

下面的 $d_s,d_p,d_o$ 分别表示在其他两个元的前提下，当前元的合理性，具体做法就是先融合另两个元，再将当前元投影到另两个元的空间中，其中的 $t_s,t_p,t_o$ 分别为主体、谓词和客体的语言学词向量表示：

$$ \left\{ \begin{aligned} d_s &= \sigma(t_p \star t_o) \odot \sigma(w_s t_s) \\ d_p &= \sigma(t_s \star t_o) \odot \sigma(w_p t_p) \\ d_o &= \sigma(t_s \star t_p) \odot \sigma(w_o t_o) \end{aligned} \right. $$

最终整体的合理性计算则是先将上述三个元的合理性拼接后，再投影到一维，用以表示某一个三元组的合理程度：

$$ d_{usrl}=w_{usrl}\left[d_s,d_p,d_o\right] $$

接着就将这个Space Reduction的过程视为一个Positive-Unlabeled Learning问题，用下面的损失进行优化，此处的正例认为是作为未见三元组的候选类，负例就视为被剔除的三元组类别，unlabeled类在此处可以理解为所有未见三元组类别：

$$ \mathcal{L}_{usrl} = \frac{\pi}{n_{pos}} \sum_{h_i} \mathcal{L}_{bce}^+(h_i) + \max \left(0, \frac{1}{n_u} \sum_{h_j} \mathcal{L}_{bce}^-(h_j) - \frac{\pi}{n_{pos}} \sum_{h_i} \mathcal{L}_{bce}^-(h_i)\right) $$

其中的 $n_{pos}, n_u$ 分别为正例和unlabeled类的数量； $\pi$ 为一个超参，表示正例所占的比例； $\mathcal{L}_{bce}^+,\mathcal{L}_{bce}^-$ 分别为分为正例与分为负例的风险，具体实现时直接用BCELoss； $h_i,h_j$ 分别为当前认为是正例、所有unlabeled样本的置信度，实现时使用上面的 $d_{usrl}$

通过优化这个Positive-Unlabeled Learning问题，可以不断缩小 $C_{tpt}^u$ 的大小，从而影响 $\mathbb{I}_m^{\alpha}\left(s,c,o\right)$ 与 $\mathbb{I}_m\left(s,c,o\right)$

实验结果

使用了Visual Genome数据集进行训练与测试，该数据集中定义了下面三种任务：

Predicate Classification：PredCls，输入图片以及实体的bbox与类别，要求输出各bbox之间的谓词关系
Scene Graph Classification：SGCls，输入图片以及实体的bbox，要求输出各实体的类别以及各bbox之间的谓词关系
Scene Graph Detection：SGDet，仅输入图片，要求输出实体的bbox与类别以及各bbox之间的谓词关系

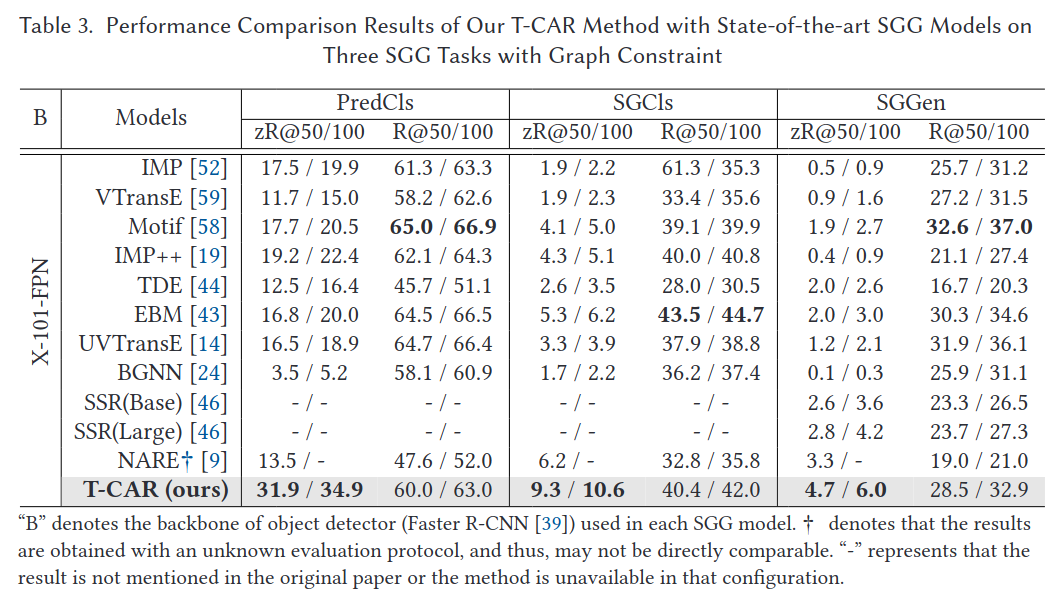
首先对比了有图约束和无图约束（with/without graph constraints）时在上述三个子任务下的zero-shot性能：

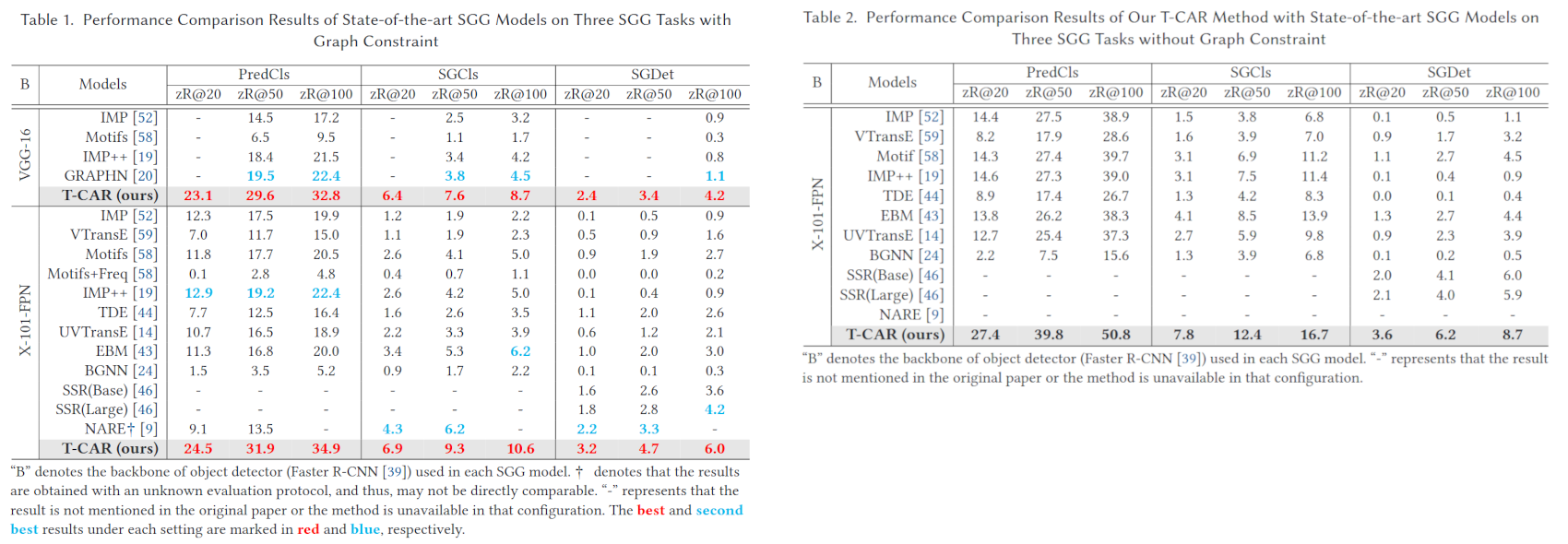
zero-shot性能对比表

也对比了非zero-shot的性能

非zero-shot性能对比

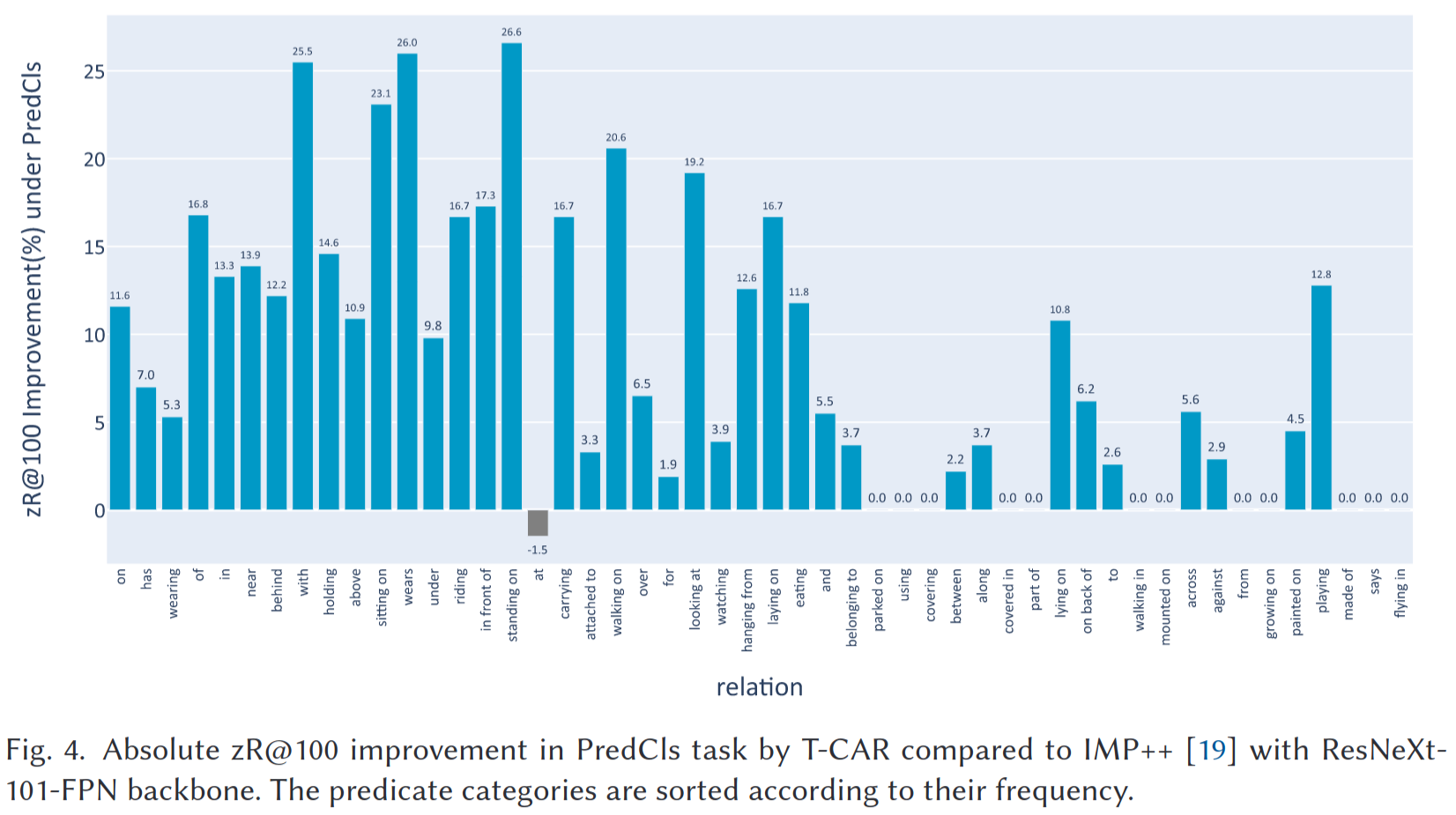
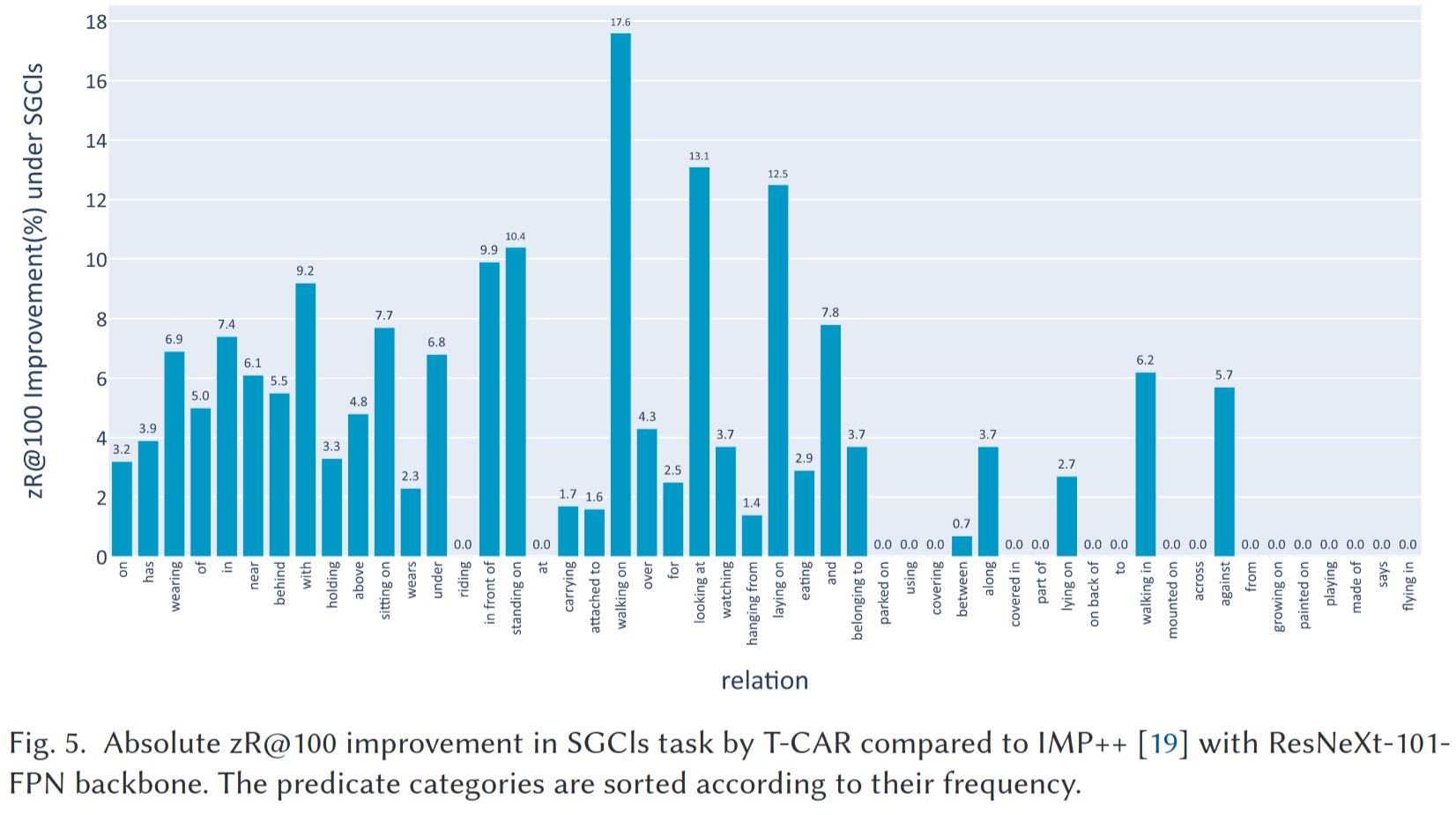
接着和IMP++模型对比了PredCls和SGCls任务中各关系类别上的zero-shot能力提高程度

PredCls上的zero-shot能力提高

SGCls上的zero-shot能力提高